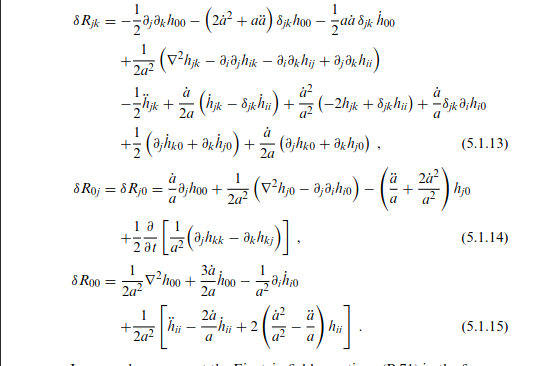Expanding sum into time and purely space components.

Question

Greetings.

1. Ricci tensor perturbations involve sum over spacetime components (in FLRW ->{t, r, \theta \varphi} ). How to expand spacetime sum (greek indices) into time and purely space components (latin indices)?
2. For each Gamma and \delta{\Gamma} there are subrules (see related image): Gamma^{t}_{t t}= ... Gamma^{t}_ {t i}=... How to setup and substitute this relations in master equations?

The core of programm is

import cdb.core.manip as mp
import cdb.core.component as cmp
{t,r, \theta, \varphi}::Coordinate.
a::Depends(t).
{\mu, \nu, \rho, \sigma, \alpha, \beta, \gamma, \lambda, \tau, \chi, \iota, \upsilon, \omega}::Indices(curved,position=fixed,values={t,r, \theta, \varphi}).
{a,b,c,d,e,f,g,i,j,k,l,m,n,p,s}::Indices(position=fixed,values={r, \theta, \varphi})
gb{#}::LaTeXForm("\bar{g}").
gb_{\mu \nu}::Symmetric.
gb::Diagonal;
{gb^{\mu}_{\nu}, gb_{\mu}^{\nu}}::KroneckerDelta.
back := gb\_\{t t\}=\-1\, gb\_\{r r\}=a**2/(1-k*r**2), gb_{\theta \theta}=a**2*r**2, gb_{\varphi \varphi}=a**2*r**2*\sin{\theta}**2, gb^{t t}=-1, gb^{r r}=(1-k*r**2)/(a**2), gb^{\theta \theta}=1/(r**2_a**2), gb^{\varphi \varphi}=1/(a**2_r\*\*2\*\sin\{\theta\}\*\*2\)\, gb\_\{t r\}=0\, gb\_\{t \theta\}=0\, gb\_\{t \varphi\}=0\, gb\_\{r \theta\}=0\, gb\_\{r \varphi\}=0\, gb\_\{\theta \varphi\}=0\, gb\_\{r t\}=0\, gb\_\{\theta t\}=0\, gb\_\{\varphi t\}=0\, gb\_\{\theta r\}=0\, gb\_\{\varphi r\}=0\, gb\_\{ \varphi \theta\}=0;

In the part we define components of ricci perturbations:

gs{#}::LaTeXForm("\overline{\gamma}")
dGamma{#}::LaTeXForm("\delta\Gamma");

dRic{#}::LaTeXForm("\delta R").
perric := \delta{R_{\mu \nu}} = \partial_{\sigma}{dGamma^{\sigma}_{\mu \nu}} - \partial_{\nu}{dGamma^{\sigma}_{\mu \sigma}} + dGamma^{\rho}_{\mu \nu} \Gamma^{\sigma}_{\rho \sigma} + \Gamma^{\rho}_{\mu \nu} dGamma^{\sigma}_{\rho \sigma} - dGamma^{\rho}_{\mu \sigma} \Gamma^{\sigma}_{\nu \rho} - \Gamma^{\rho}_{\mu \sigma} dGamma^{\sigma}_{\nu \rho};

dr1 = cmp.get_component(perric, $t,t$);
dr2 = cmp.get_component(perric, $t,i$);
dr3 = cmp.get_component(perric, $j,k$);

How to expand sum?

We try to define relation for non perturbed Gamma!:

eq1 := {\Gamma}^{t}_{i j}=(a \partial_{t}{a} {gs}_{i j});

But error appear: RuntimeError: Free indices on lhs and rhs do not match.

Thank you in advance for your help.

Answer 1

Hi Heckfy.

This "anwser" is more a comment, but it might transform onto an answer after some discussion.

First contact

I understand what you are trying to achieve, but not your question specifically. Let me comment further.

• There are typographic in your code blocks, and missing components in your substitution rules (non-diagonal inverse components of the background metric).

I think that the right substitution rule should be

back := gb_{t t}=-1, 
  gb_{r r}=a**2/(1-k*r**2), 
  gb_{\theta \theta}=a**2*r**2, 
  gb_{\varphi \varphi}=a**2*r**2*\sin{\theta}**2, 
  gb_{t r}=0, 
  gb_{t \theta}=0, 
  gb_{t \varphi}=0, 
  gb_{r \theta}=0, 
  gb_{r \varphi}=0, 
  gb_{\theta \varphi}=0,
  gb_{r t}=0, 
  gb_{\theta t}=0,
  gb_{\varphi t}=0,
  gb_{\theta r}=0,
  gb_{\varphi r}=0, 
  gb_{\varphi \theta}=0
  gb^{t t}=-1, 
  gb^{r r}=(1-k*r**2)/(a**2), 
  gb^{\theta \theta}=1/(r**2 * a**2), 
  gb^{\varphi \varphi}=1/(a**2 * r**2 *\sin{\theta}**2), 
  gb^{t r}=0, 
  gb^{t \theta}=0, 
  gb^{t \varphi}=0, 
  gb^{r \theta}=0, 
  gb^{r \varphi}=0, 
  gb^{\theta \varphi}=0,
  gb^{r t}=0, 
  gb^{\theta t}=0,
  gb^{\varphi t}=0,
  gb^{\theta r}=0,
  gb^{\varphi r}=0, 
  gb^{\varphi \theta}=0;

• In your question you talk about the connection and Ricci tensor, but there is nothing in the presented code referring to those objects. Could you please update the post to include a more complete notebook?
• The second code block in your post does not compute anything! Remind that cadabra is not a calculation software, but a manipulation software. That means that you have to tell it explicitly what to do. So far (at least in what you showed), it is doing nothing.

Well, in short, could you improve the quality of your post: improve the statement of your question, and provide a more complete version of your code.

Cheers, Dox.